
I found it useful to compare to the old PCs that I used for my work (almost a hundred times faster!) or against other smartphones (similar to other what I see quoted for other ARM chips at similar clock speeds). In that sense, Linpack is useful for getting a rough notion of the iPhone's power on math-intensive work and almost nothing else. I've used the math on desktop machines for an aggressive stat approach to investing, and the math has useful applications in almost all science, but a phone, especially due to its casual use patterns, is an unlikely home for these types of in-depth studies. (That is, IF it worked against real data and reported any result other than how accurately it solved the linpack problem. I am not aware of any app that actually uses this type of math on a smartphone most smartphone applications, even if they analyze huge sets of data, don't attempt the advanced statistical insights it could give. Linpack is a benchmark program with a long history this little app moves it to the iPhone. The relative machine precision usually the smallest positive number such that fl( 1.0 - eps ) < 1.0, where fl denotes the computed value and eps is the relative machine precision.ĭoes what it says: a very specialized test of math speed If this quantity is much larger than 1, the solution is probably incorrect. The Norm Res should be about O(1) in size. The test is based on || Ax - b || / ( || A || || x || eps) where eps is described below. The time in seconds to solve the problem, Ax=b.Ī check is made to show that the computed solution is correct.
For this problem there are 2/3 n^3 + n^2 floating point operations. A floating point operation here is a floating point addition or a floating point multiplication with 64 bit operands. Millions of floating point operations per second. The result is reported in millions of floating point operations per second (MFLOP/s, sometimes simply called FLOPS).

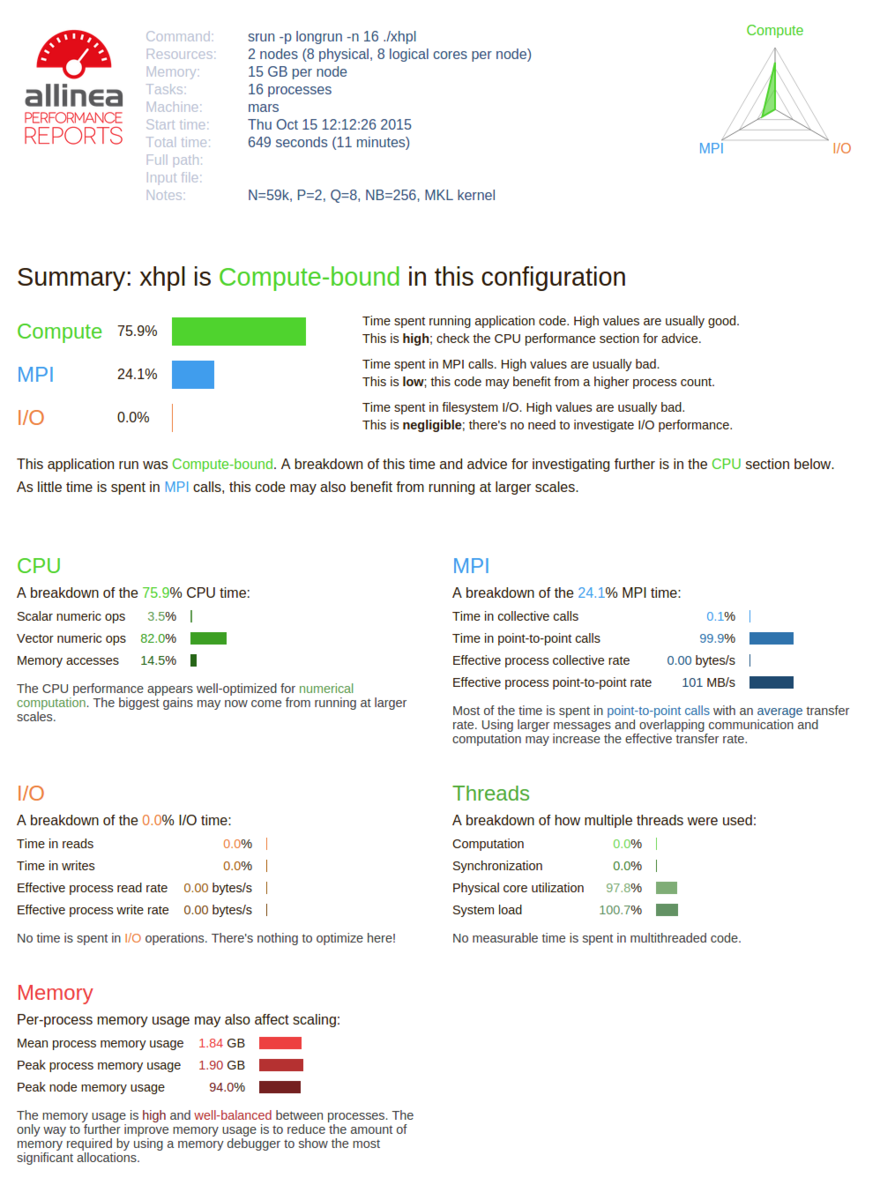
The solution is obtained by Gaussian elimination with partial pivoting, with 2/3 They measure how fast a computer solves a dense N by N system of linear equations Ax = b, which is a common task in engineering.

The LINPACK Benchmarks are a measure of a system's floating point computing power.


 0 kommentar(er)
0 kommentar(er)
